阅读本文需要一些前置知识,需理解向量点积与叉积的基本知识。以下给出大致定义(因为矩阵在这里用不到,就不写矩阵形式了)以帮助理解
向量点积
v ⃗ ⋅ j ⃗ = ∣ ∣ v ⃗ ∣ ∣ ∣ ∣ j ⃗ ∣ ∣ cos θ \vec {v} \cdot \vec {j} = ||\vec {v}|| ||\vec {j}|| \cos \theta v ⋅ j = ∣∣ v ∣∣∣∣ j ∣∣ cos θ 几何解释为 向量 v 在 向量 j 上投影的模长乘以向量 j 的模长
向量叉积
v ⃗ × j ⃗ = ∣ ∣ v ⃗ ∣ ∣ ∣ ∣ j ⃗ ∣ ∣ sin θ \vec {v} \times \vec {j} = ||\vec {v}|| ||\vec {j}|| \sin \theta v × j = ∣∣ v ∣∣∣∣ j ∣∣ sin θ 叉积只有在三维下才有几何意义,其解释为同时与向量 v 与向量 j 垂直的向量,且该向量模长为向量 v 与向量 j 构成的平行四边形的面积
另外需要注意的是,本文基于右手系分析,旋转方向正负可由右手定则判断。
罗德里格旋转公式#
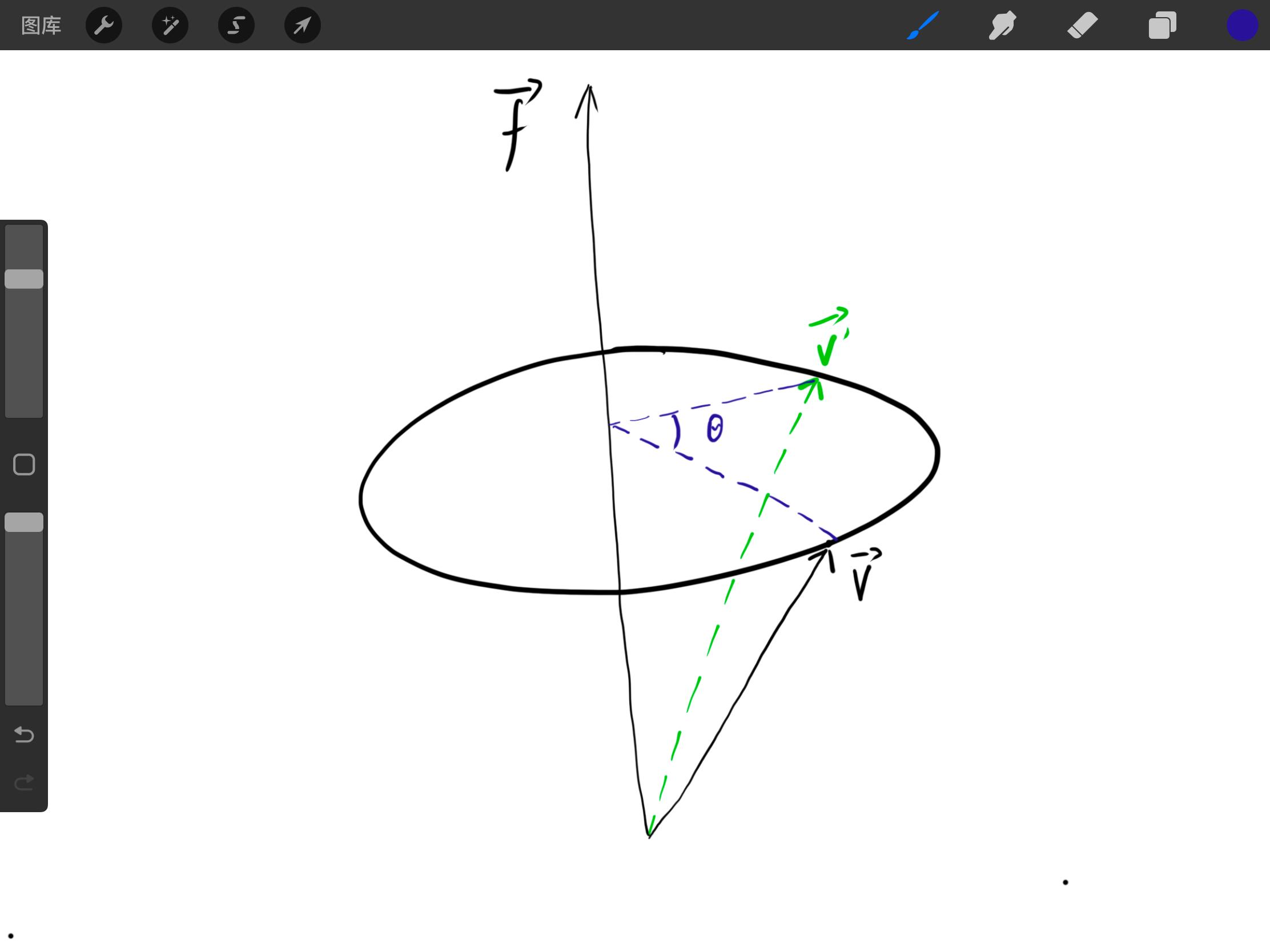
已知旋转轴 f ⃗ \vec{f} f v ⃗ \vec{v} v θ \theta θ v ′ ⃗ \vec {v^{\prime}} v ′
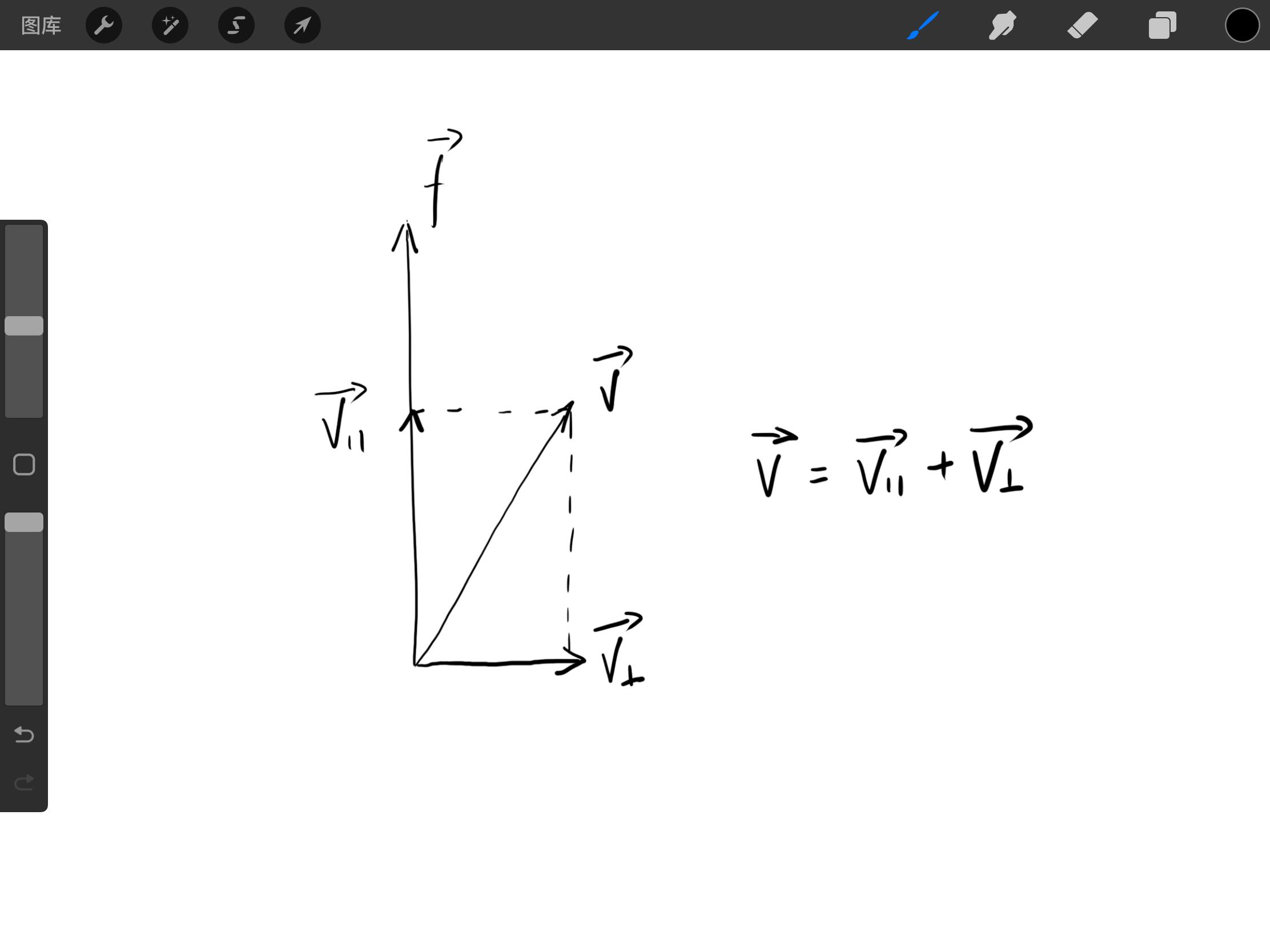
因为旋转轴的长度并不影响旋转,为了方便求解,定义 ∣ ∣ f ⃗ ∣ ∣ = 1 ||\vec {f}|| = 1 ∣∣ f ∣∣ = 1 v ⃗ \vec {v} v v ∥ ⃗ \vec {v_\parallel} v ∥ v ⊥ ⃗ \vec {v_\perp} v ⊥
由于 v ∥ ⃗ \vec{v_\parallel} v ∥ v ⃗ \vec{v} v f ⃗ \vec{f} f
即 v ∥ ⃗ = v ⃗ ⋅ f ⃗ ∣ ∣ f ⃗ ∣ ∣ f ⃗ ∣ ∣ f ⃗ ∣ ∣ \vec {v_\parallel} = \frac{\vec {v} \cdot \vec {f}}{||\vec {f}||} \frac {\vec {f}}{||\vec {f}||} v ∥ = ∣∣ f ∣∣ v ⋅ f ∣∣ f ∣∣ f
这里解释一下为什么这么写,上面对于点积的介绍已经很明确了即点积的结果表示为向量 v 在 向量 f 上投影的模长乘以向量 f 的模长,也就说我们如果需要单独获得 ∣ ∣ v ∥ ⃗ ∣ ∣ || \vec {v_\parallel} || ∣∣ v ∥ ∣∣ ∣ ∣ f ⃗ ∣ ∣ ||\vec {f}|| ∣∣ f ∣∣ v ∥ ⃗ ∥ f ⃗ \vec {v_\parallel} \parallel \vec {f} v ∥ ∥ f f ⃗ \vec {f} f v ∥ ⃗ \vec {v_\parallel} v ∥ ∣ ∣ f ⃗ ∣ ∣ ||\vec {f}|| ∣∣ f ∣∣
Copy v ∥ ⃗ = ( v ⃗ ⋅ f ⃗ ) f ⃗ \vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f} v ∥ = ( v ⋅ f ) f 此时也可以得到 v ⊥ ⃗ \vec {v_\perp} v ⊥
v ⊥ ⃗ = v ⃗ − v ∥ ⃗ = v ⃗ − ( v ⃗ ⋅ f ⃗ ) f ⃗ \vec {v_\perp} = \vec {v} - \vec {v_\parallel} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f} v ⊥ = v − v ∥ = v − ( v ⋅ f ) f
目前已经得到的结果
Copy { v ∥ ⃗ = ( v ⃗ ⋅ f ⃗ ) f ⃗ v ⊥ ⃗ = v ⃗ − ( v ⃗ ⋅ f ⃗ ) f ⃗ \begin{cases}
\vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f} \\
\vec {v_\perp} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f}
\end{cases} { v ∥ = ( v ⋅ f ) f v ⊥ = v − ( v ⋅ f ) f 现在我们对 v ′ ⃗ \vec {v^{\prime}} v ′ v ∥ ⃗ = v ∥ ′ ⃗ \vec {v_\parallel} = \vec {v^{\prime}_\parallel} v ∥ = v ∥ ′
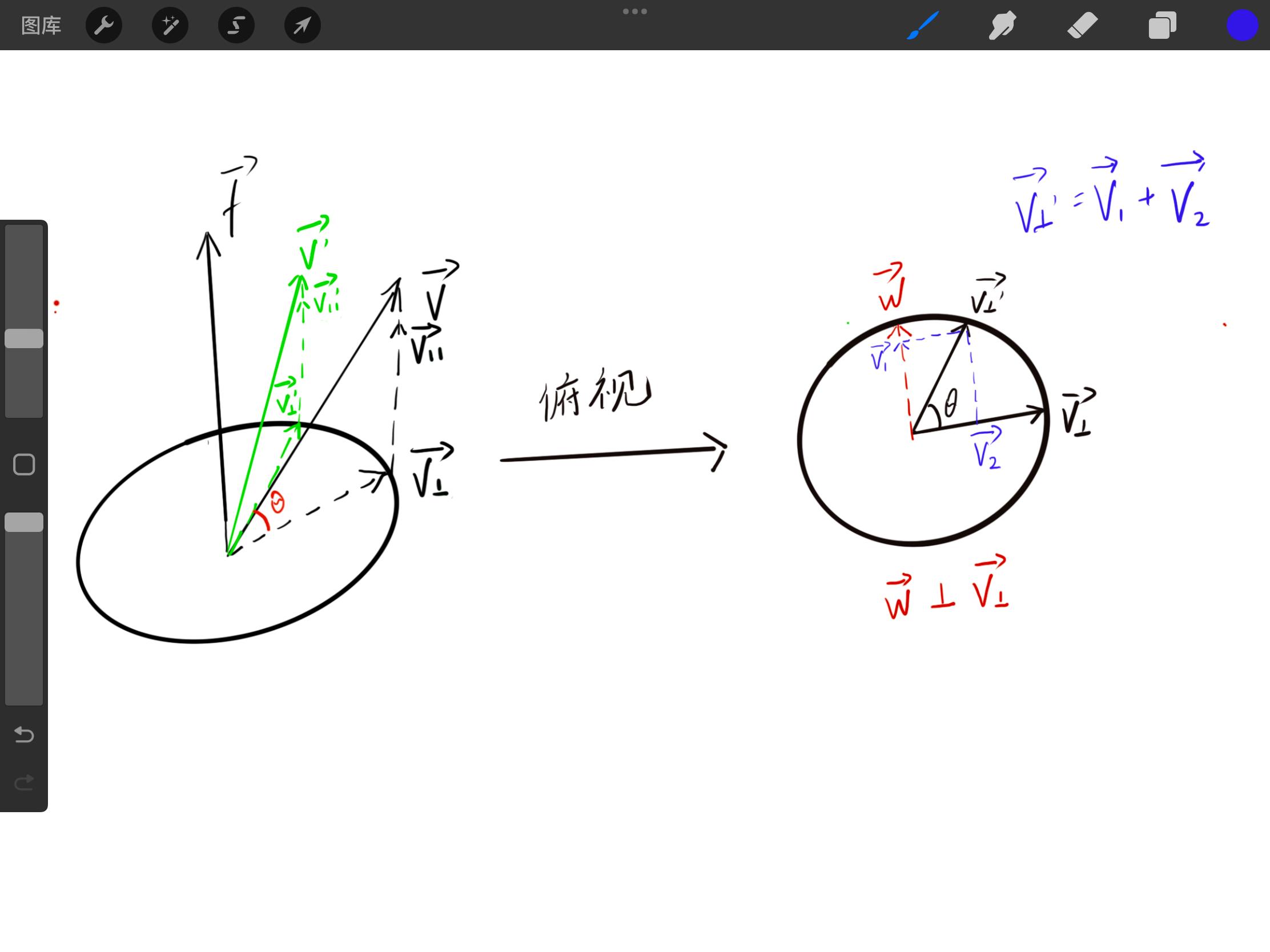
此时我们引入辅助向量 w ⃗ \vec {w} w v ⊥ ⃗ \vec {v_\perp} v ⊥
Copy ∵ { w ⃗ ⊥ f ⃗ w ⃗ ⊥ v ⊥ ⃗ ∣ ∣ f ⃗ ∣ ∣ = 1 ∣ ∣ w ⃗ ∣ ∣ = ∣ ∣ v ⊥ ⃗ ∣ ∣ \because
\begin{cases}
\vec {w} \perp \vec {f} \\
\vec {w} \perp \vec {v_\perp} \\
|| \vec {f} || = 1 \\
|| \vec {w} || = || \vec {v_\perp} || \\
\end{cases} ∵ ⎩ ⎨ ⎧ w ⊥ f w ⊥ v ⊥ ∣∣ f ∣∣ = 1 ∣∣ w ∣∣ = ∣∣ v ⊥ ∣∣ Copy ∴ w ⃗ = f ⃗ × v ⊥ ⃗ \therefore
\vec {w} = \vec {f} \times \vec {v_\perp} ∴ w = f × v ⊥ 因为我们最终的目标是通过 v ⊥ ′ ⃗ \vec {v^{\prime}_\perp} v ⊥ ′ v ′ ⃗ \vec {v^{\prime}} v ′ v ⊥ ′ ⃗ \vec {v^{\prime}_\perp} v ⊥ ′ v 1 ⃗ \vec {v_1} v 1 v 2 ⃗ \vec {v_2} v 2 w ⃗ \vec {w} w v ⊥ ⃗ \vec {v_\perp} v ⊥
v 1 ⃗ = v ⊥ ′ ⃗ ⋅ w ⃗ ∣ ∣ w ⃗ ∣ ∣ w ⃗ ∣ ∣ w ⃗ ∣ ∣ = ∣ ∣ v ⊥ ′ ⃗ ∣ ∣ ∣ ∣ w ⃗ ∣ ∣ cos ( 90 ° − θ ) ∣ ∣ w ⃗ ∣ ∣ w ⃗ ∣ ∣ w ⃗ ∣ ∣ = w ⃗ sin θ \vec {v_1} = \frac {\vec {v^{\prime}_\perp} \cdot \vec {w}}{||\vec {w}||} \frac {\vec {w}}{||\vec {w}||} = \frac {||\vec {v^{\prime}_\perp}|| || \vec {w} || \cos(90° - \theta)}{|| \vec {w} ||} \frac {\vec {w}}{||\vec {w}||} = \vec {w} \sin\theta v 1 = ∣∣ w ∣∣ v ⊥ ′ ⋅ w ∣∣ w ∣∣ w = ∣∣ w ∣∣ ∣∣ v ⊥ ′ ∣∣∣∣ w ∣∣ c o s ( 90° − θ ) ∣∣ w ∣∣ w = w sin θ
v 2 ⃗ = v ⊥ ′ ⃗ ⋅ v ⊥ ⃗ ∣ ∣ v ⊥ ⃗ ∣ ∣ v ⊥ ⃗ ∣ ∣ v ⊥ ⃗ ∣ ∣ = ∣ ∣ v ⊥ ′ ⃗ ∣ ∣ ∣ ∣ v ⊥ ⃗ ∣ ∣ cos ( θ ) ∣ ∣ v ⊥ ⃗ ∣ ∣ v ⊥ ⃗ ∣ ∣ v ⊥ ⃗ ∣ ∣ = v ⊥ ⃗ cos θ \vec {v_2} = \frac {\vec {v^{\prime}_\perp} \cdot \vec {v_\perp}}{||\vec {v_\perp}||} \frac {\vec {v_\perp}}{||\vec {v_\perp}||} = \frac {||\vec {v^{\prime}_\perp}|| || \vec {v_\perp} || \cos(\theta)}{|| \vec {v_\perp} ||} \frac {\vec {v_\perp}}{||\vec {v_\perp}||} = \vec {v_\perp} \cos\theta v 2 = ∣∣ v ⊥ ∣∣ v ⊥ ′ ⋅ v ⊥ ∣∣ v ⊥ ∣∣ v ⊥ = ∣∣ v ⊥ ∣∣ ∣∣ v ⊥ ′ ∣∣∣∣ v ⊥ ∣∣ c o s ( θ ) ∣∣ v ⊥ ∣∣ v ⊥ = v ⊥ cos θ
v ⊥ ′ ⃗ = v 1 ⃗ + v 2 ⃗ = w ⃗ sin θ + v ⊥ ⃗ cos θ \vec {v^{\prime}_\perp} = \vec {v_1} + \vec {v_2} = \vec {w} \sin\theta + \vec {v_\perp} \cos\theta v ⊥ ′ = v 1 + v 2 = w sin θ + v ⊥ cos θ
∵ w ⃗ = f ⃗ × v ⊥ ⃗ \because \vec {w} = \vec {f} \times \vec {v_\perp} ∵ w = f × v ⊥
∴ v ⊥ ′ ⃗ = v ⊥ ⃗ cos θ + ( f ⃗ × v ⊥ ⃗ ) sin θ \therefore \vec {v^{\prime}_\perp} = \vec {v_\perp} \cos\theta + (\vec {f} \times \vec {v_\perp}) \sin \theta ∴ v ⊥ ′ = v ⊥ cos θ + ( f × v ⊥ ) sin θ
v ′ ⃗ = v ⊥ ′ ⃗ + v ∥ ′ ⃗ = v ⊥ ⃗ cos θ + ( f ⃗ × ( v ⃗ − v ∥ ⃗ ) ) sin θ + v ∥ ⃗ \vec {v^{\prime}} = \vec {v^{\prime}_\perp} + \vec {v^{\prime}_\parallel} = \vec {v_\perp} \cos\theta + (\vec {f} \times (\vec {v} - \vec {v_\parallel})) \sin \theta + \vec {v_\parallel} v ′ = v ⊥ ′ + v ∥ ′ = v ⊥ cos θ + ( f × ( v − v ∥ )) sin θ + v ∥
∵ f ⃗ ∥ v ∥ ⃗ ∴ f ⃗ × v ∥ ⃗ = 0 \because \vec {f} \parallel \vec {v_\parallel} \therefore \vec {f} \times \vec {v_\parallel} = 0 ∵ f ∥ v ∥ ∴ f × v ∥ = 0
v ′ ⃗ = v ∥ ⃗ + cos θ v ⊥ ⃗ + ( f ⃗ × v ⃗ ) sin θ \vec {v^{\prime}} = \vec {v_\parallel} + \cos \theta \vec {v_\perp} + (\vec {f} \times \vec {v}) \sin \theta v ′ = v ∥ + cos θ v ⊥ + ( f × v ) sin θ
Copy ∵ { v ∥ ⃗ = ( v ⃗ ⋅ f ⃗ ) f ⃗ v ⊥ ⃗ = v ⃗ − ( v ⃗ ⋅ f ⃗ ) f ⃗ \because
\begin{cases}
\vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f} \\
\vec {v_\perp} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f}
\end{cases} ∵ { v ∥ = ( v ⋅ f ) f v ⊥ = v − ( v ⋅ f ) f ∴ v ′ ⃗ = ( 1 − cos θ ) ( f ⃗ ⋅ v ⃗ ) f ⃗ + cos θ v ⃗ + sin θ ( f ⃗ × v ⃗ ) \therefore \vec {v^{\prime}} = (1 - \cos \theta)(\vec {f} \cdot \vec {v}) \vec {f} + \cos \theta \vec {v} + \sin \theta (\vec {f} \times \vec {v}) ∴ v ′ = ( 1 − cos θ ) ( f ⋅ v ) f + cos θ v + sin θ ( f × v )
求证结束,此时我们得到了轴角式的旋转公式。
参考资料#
《动手学机器人学》(5)(一般形式旋转矩阵公式)或(罗德里格旋转公式)或(轴角法)证明 and 齐次坐标变换