banner
IWSR

IWSR

我永远喜欢志喜屋梦子！
ホームアーカイブ

ロドリゲスの回転公式（軸角法）

#数学#图形学354
AI 翻訳
この記事はAIを通じて英語から日本語に翻訳されました。原文を表示
AI が生成した要約
本文介绍了罗德里格旋转公式，该公式用于求解已知旋转轴和旋转角度的情况下，求旋转后的向量。文章首先介绍了向量点积和叉积的定义和几何解释，然后引入了右手系和旋转方向的概念。接着详细推导了罗德里格旋转公式，包括将向量分解到平面和旋转轴上，引入辅助向量，以及分解旋转后的向量到平面上的两个分量。最后得出了轴角式的旋转公式。

序文#

この記事を読むには、ベクトルの内積と外積の基本的な知識を理解する必要があります。以下に、大まかな定義を示します（ここでは行列は使用しないため、行列形式は書きません）。

  • ベクトルの内積
    • v⃗⋅j⃗=∣∣v⃗∣∣∣∣j⃗∣∣cos⁡θ\vec {v} \cdot \vec {j} = ||\vec {v}|| ||\vec {j}|| \cos \theta
    • 幾何学的には、ベクトル v をベクトル j に投影した長さにベクトル j の長さを掛けたものです。
  • ベクトルの外積
    • v⃗×j⃗=∣∣v⃗∣∣∣∣j⃗∣∣sin⁡θ\vec {v} \times \vec {j} = ||\vec {v}|| ||\vec {j}|| \sin \theta
    • 外積は三次元空間でのみ幾何学的な意味を持ち、ベクトル v とベクトル j に直交するベクトルであり、その大きさはベクトル v とベクトル j が作る平行四辺形の面積です。

また、注意する必要があるのは、この記事は右手系を基にしており、回転方向の正負は右手の法則で判断できます。

右手系 右手の法則

ロドリゲスの回転公式#

回転軸 f⃗\vec{f} が与えられた場合、ベクトル v⃗\vec{v} を回転軸周りに θ\theta 角回転させた後の v′⃗\vec {v^{\prime}} を求めます。以下の図を参照してください。

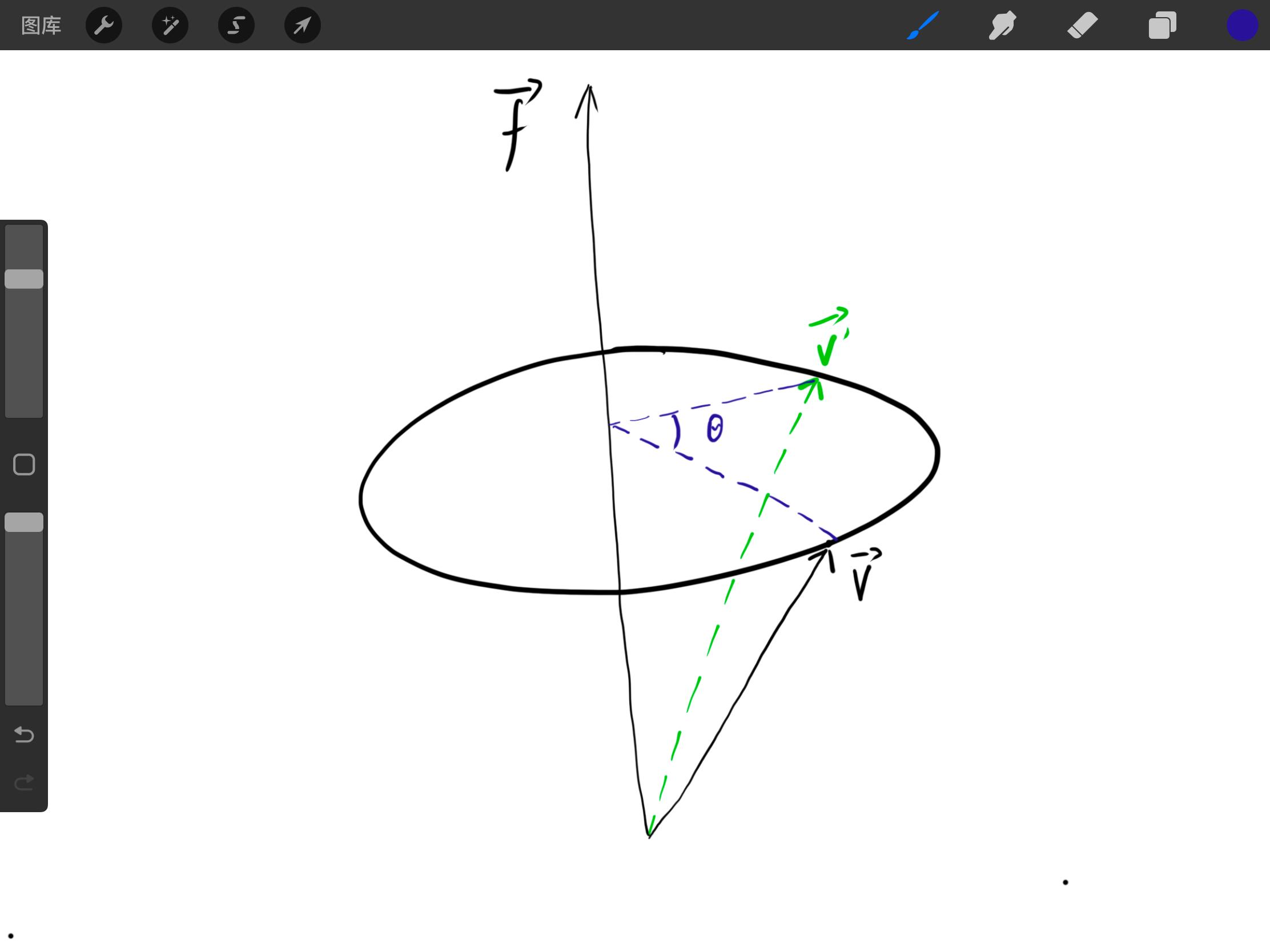
IMG_ECC68942A572-1

回転軸の長さは回転に影響を与えないため、解を求めるために、 ∣∣f⃗∣∣=1||\vec {f}|| = 1 と定義します。この時、平面（ v∥⃗\vec {v_\parallel} ）と回転軸（ v⊥⃗\vec {v_\perp} ）に v⃗\vec {v} を分解します。以下の図を参照してください。

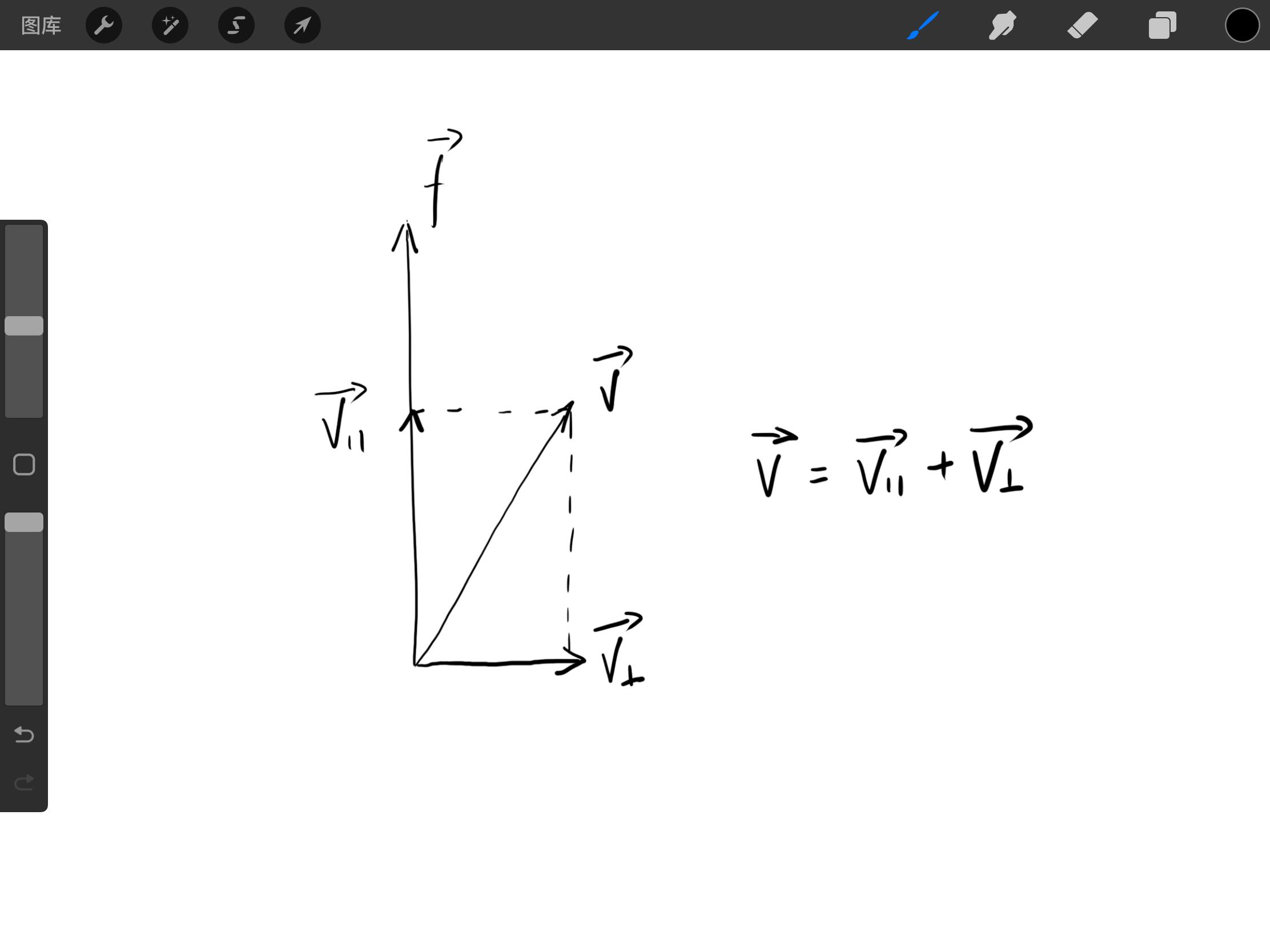
IMG_D190DB86E9D2-1

v∥⃗\vec{v_\parallel} は、 v⃗\vec{v} を f⃗\vec{f} 上に射影したものと見なすことができます。明らかに、内積を使用して表すことができます。

すなわち、 v∥⃗=v⃗⋅f⃗∣∣f⃗∣∣f⃗∣∣f⃗∣∣\vec {v_\parallel} = \frac{\vec {v} \cdot \vec {f}}{||\vec {f}||} \frac {\vec {f}}{||\vec {f}||}

ここで、なぜこのように書くのかについて説明します。上記の内積の説明は非常に明確です。内積の結果は、ベクトル v をベクトル f に投影した長さにベクトル f の長さを掛けたものです。つまり、 ∣∣v∥⃗∣∣|| \vec {v_\parallel} || を単独で取得する場合、結果を ∣∣f⃗∣∣||\vec {f}|| で除算する必要があります。この時、ベクトルではなく値が得られます。また、 v∥⃗∥f⃗\vec {v_\parallel} \parallel \vec {f} であることに注意してください。つまり、2 つのベクトルは同じ方向を向いています。したがって、値に f⃗\vec {f} を掛けることで、 v∥⃗\vec {v_\parallel} を得ることができます。また、 ∣∣f⃗∣∣||\vec {f}|| は 1 であるため、次のように簡略化できます。

v∥⃗=(v⃗⋅f⃗)f⃗\vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f}

この時点で、 v⊥⃗\vec {v_\perp} も得ることができます。

v⊥⃗=v⃗−v∥⃗=v⃗−(v⃗⋅f⃗)f⃗\vec {v_\perp} = \vec {v} - \vec {v_\parallel} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f}

現在、次の結果が得られています。

{v∥⃗=(v⃗⋅f⃗)f⃗v⊥⃗=v⃗−(v⃗⋅f⃗)f⃗\begin{cases} \vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f} \\ \vec {v_\perp} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f} \end{cases}

次に、 v′⃗\vec {v^{\prime}} を分解します。 v∥⃗=v∥′⃗\vec {v_\parallel} = \vec {v^{\prime}_\parallel} であることに気づくことができますが、平面上での分解が異なります。

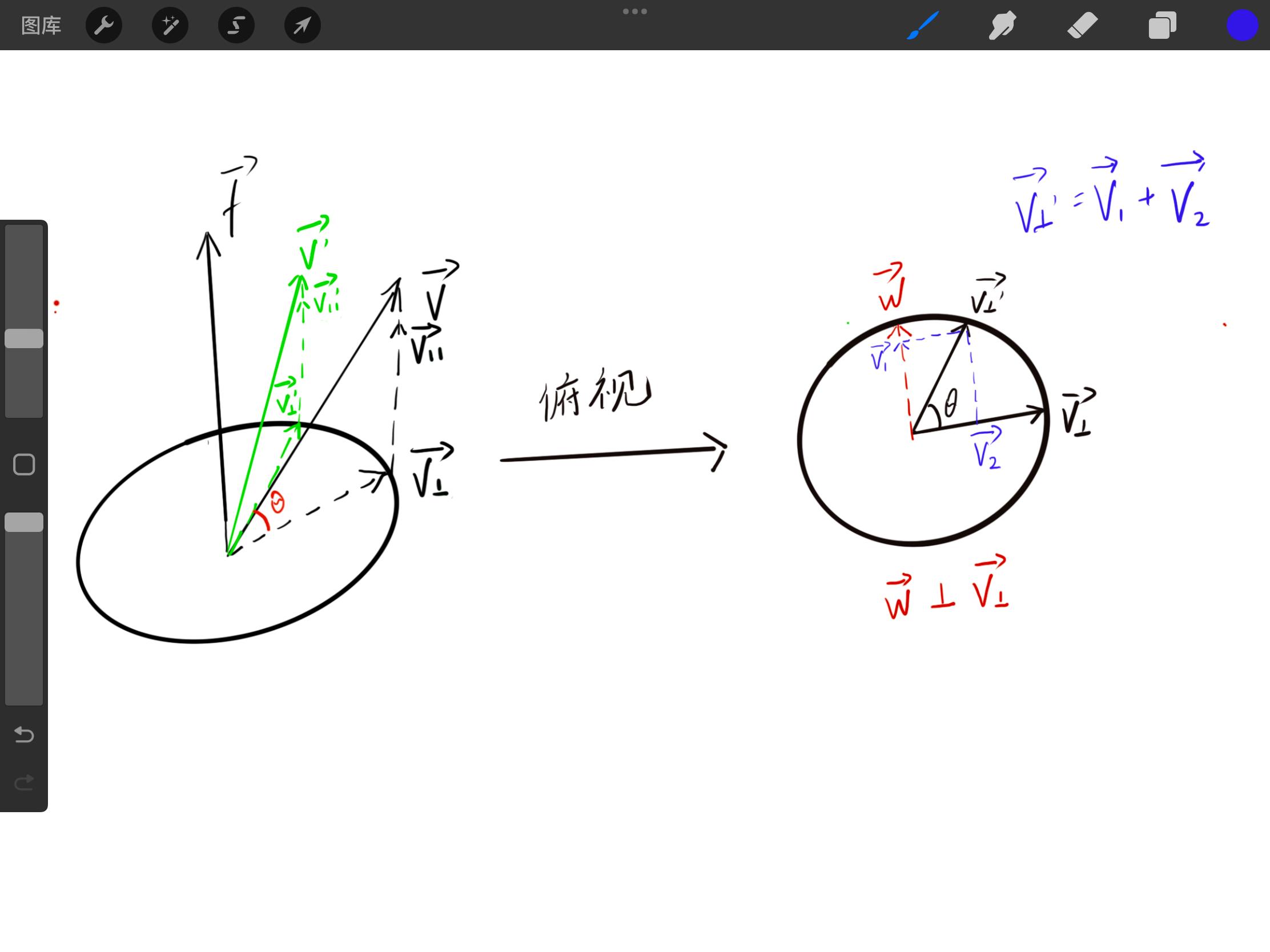
IMG_8ADF34270E8C-1

この時、補助ベクトル w⃗\vec {w} を導入します。このベクトルは v⊥⃗\vec {v_\perp} に垂直です。

∵{w⃗⊥f⃗w⃗⊥v⊥⃗∣∣f⃗∣∣=1∣∣w⃗∣∣=∣∣v⊥⃗∣∣\because \begin{cases} \vec {w} \perp \vec {f} \\ \vec {w} \perp \vec {v_\perp} \\ || \vec {f} || = 1 \\ || \vec {w} || = || \vec {v_\perp} || \\ \end{cases}
∴w⃗=f⃗×v⊥⃗\therefore \vec {w} = \vec {f} \times \vec {v_\perp}

最終的な目標は、 v⊥′⃗\vec {v^{\prime}_\perp} を使用して v′⃗\vec {v^{\prime}} を求めることです。そのためには、 v⊥′⃗\vec {v^{\prime}_\perp} を v1⃗\vec {v_1} と v2⃗\vec {v_2} に分解し、既知の w⃗\vec {w} と v⊥⃗\vec {v_\perp} を使用して表現する必要があります（v 平行と同じ解法です）。

v1⃗=v⊥′⃗⋅w⃗∣∣w⃗∣∣w⃗∣∣w⃗∣∣=∣∣v⊥′⃗∣∣∣∣w⃗∣∣cos⁡(90°−θ)∣∣w⃗∣∣w⃗∣∣w⃗∣∣=w⃗sin⁡θ\vec {v_1} = \frac {\vec {v^{\prime}_\perp} \cdot \vec {w}}{||\vec {w}||} \frac {\vec {w}}{||\vec {w}||} = \frac {||\vec {v^{\prime}_\perp}|| || \vec {w} || \cos(90° - \theta)}{|| \vec {w} ||} \frac {\vec {w}}{||\vec {w}||} = \vec {w} \sin\theta

v2⃗=v⊥′⃗⋅v⊥⃗∣∣v⊥⃗∣∣v⊥⃗∣∣v⊥⃗∣∣=∣∣v⊥′⃗∣∣∣∣v⊥⃗∣∣cos⁡(θ)∣∣v⊥⃗∣∣v⊥⃗∣∣v⊥⃗∣∣=v⊥⃗cos⁡θ\vec {v_2} = \frac {\vec {v^{\prime}_\perp} \cdot \vec {v_\perp}}{||\vec {v_\perp}||} \frac {\vec {v_\perp}}{||\vec {v_\perp}||} = \frac {||\vec {v^{\prime}_\perp}|| || \vec {v_\perp} || \cos(\theta)}{|| \vec {v_\perp} ||} \frac {\vec {v_\perp}}{||\vec {v_\perp}||} = \vec {v_\perp} \cos\theta

v⊥′⃗=v1⃗+v2⃗=w⃗sin⁡θ+v⊥⃗cos⁡θ\vec {v^{\prime}_\perp} = \vec {v_1} + \vec {v_2} = \vec {w} \sin\theta + \vec {v_\perp} \cos\theta

∵w⃗=f⃗×v⊥⃗\because \vec {w} = \vec {f} \times \vec {v_\perp}

∴v⊥′⃗=v⊥⃗cos⁡θ+(f⃗×v⊥⃗)sin⁡θ\therefore \vec {v^{\prime}_\perp} = \vec {v_\perp} \cos\theta + (\vec {f} \times \vec {v_\perp}) \sin \theta

v′⃗=v⊥′⃗+v∥′⃗=v⊥⃗cos⁡θ+(f⃗×(v⃗−v∥⃗))sin⁡θ+v∥⃗\vec {v^{\prime}} = \vec {v^{\prime}_\perp} + \vec {v^{\prime}_\parallel} = \vec {v_\perp} \cos\theta + (\vec {f} \times (\vec {v} - \vec {v_\parallel})) \sin \theta + \vec {v_\parallel}

∵f⃗∥v∥⃗∴f⃗×v∥⃗=0\because \vec {f} \parallel \vec {v_\parallel} \therefore \vec {f} \times \vec {v_\parallel} = 0

v′⃗=v∥⃗+cos⁡θv⊥⃗+(f⃗×v⃗)sin⁡θ\vec {v^{\prime}} = \vec {v_\parallel} + \cos \theta \vec {v_\perp} + (\vec {f} \times \vec {v}) \sin \theta

∵{v∥⃗=(v⃗⋅f⃗)f⃗v⊥⃗=v⃗−(v⃗⋅f⃗)f⃗\because \begin{cases} \vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f} \\ \vec {v_\perp} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f} \end{cases}

∴v′⃗=(1−cos⁡θ)(f⃗⋅v⃗)f⃗+cos⁡θv⃗+sin⁡θ(f⃗×v⃗) \therefore \vec {v^{\prime}} = (1 - \cos \theta)(\vec {f} \cdot \vec {v}) \vec {f} + \cos \theta \vec {v} + \sin \theta (\vec {f} \times \vec {v})

証明終了、これで軸角度の回転公式が得られました。

参考文献#

《动手学机器人学》（5）（一般形式旋转矩阵公式）或（罗德里格旋转公式）或（轴角法）证明 and 齐次坐标变换

読み込み中...
文章は、創作者によって署名され、ブロックチェーンに安全に保存されています。