banner
IWSR

IWSR

我永远喜欢志喜屋梦子！
首頁封存

羅德里格旋轉公式（軸角法）

#数学#图形学354
AI 翻譯
這篇文章透過AI由英文翻譯成繁體中文。查看原文
AI 生成的摘要
本文介紹了向量的點積和叉積的基本知識，並解釋了羅德里格旋轉公式的推導過程。點積表示向量在另一向量上的投影，叉積在三維空間中有幾何意義。文章基於右手系分析，並提供了相關參考資料。

前言#

閱讀本文需要一些前置知識，需理解向量點積與叉積的基本知識。以下給出大致定義（因為矩陣在這裡用不到，就不寫矩陣形式了）以幫助理解

  • 向量點積
    • v⃗⋅j⃗=∣∣v⃗∣∣∣∣j⃗∣∣cos⁡θ\vec {v} \cdot \vec {j} = ||\vec {v}|| ||\vec {j}|| \cos \theta
    • 幾何解釋為 向量 v 在 向量 j 上投影的模長乘以向量 j 的模長
  • 向量叉積
    • v⃗×j⃗=∣∣v⃗∣∣∣∣j⃗∣∣sin⁡θ\vec {v} \times \vec {j} = ||\vec {v}|| ||\vec {j}|| \sin \theta
    • 叉積只有在三維下才有幾何意義，其解釋為同時與向量 v 與向量 j 垂直的向量，且該向量模長為向量 v 與向量 j 構成的平行四邊形的面積

另外需要注意的是，本文基於右手系分析，旋轉方向正負可由右手定則判斷。

右手系 右手定則

羅德里格旋轉公式#

已知旋轉軸 f⃗\vec{f} ，此時有向量 v⃗\vec{v} 繞旋轉軸旋轉 θ\theta 角，求旋轉後的 v′⃗\vec {v^{\prime}}。如下圖

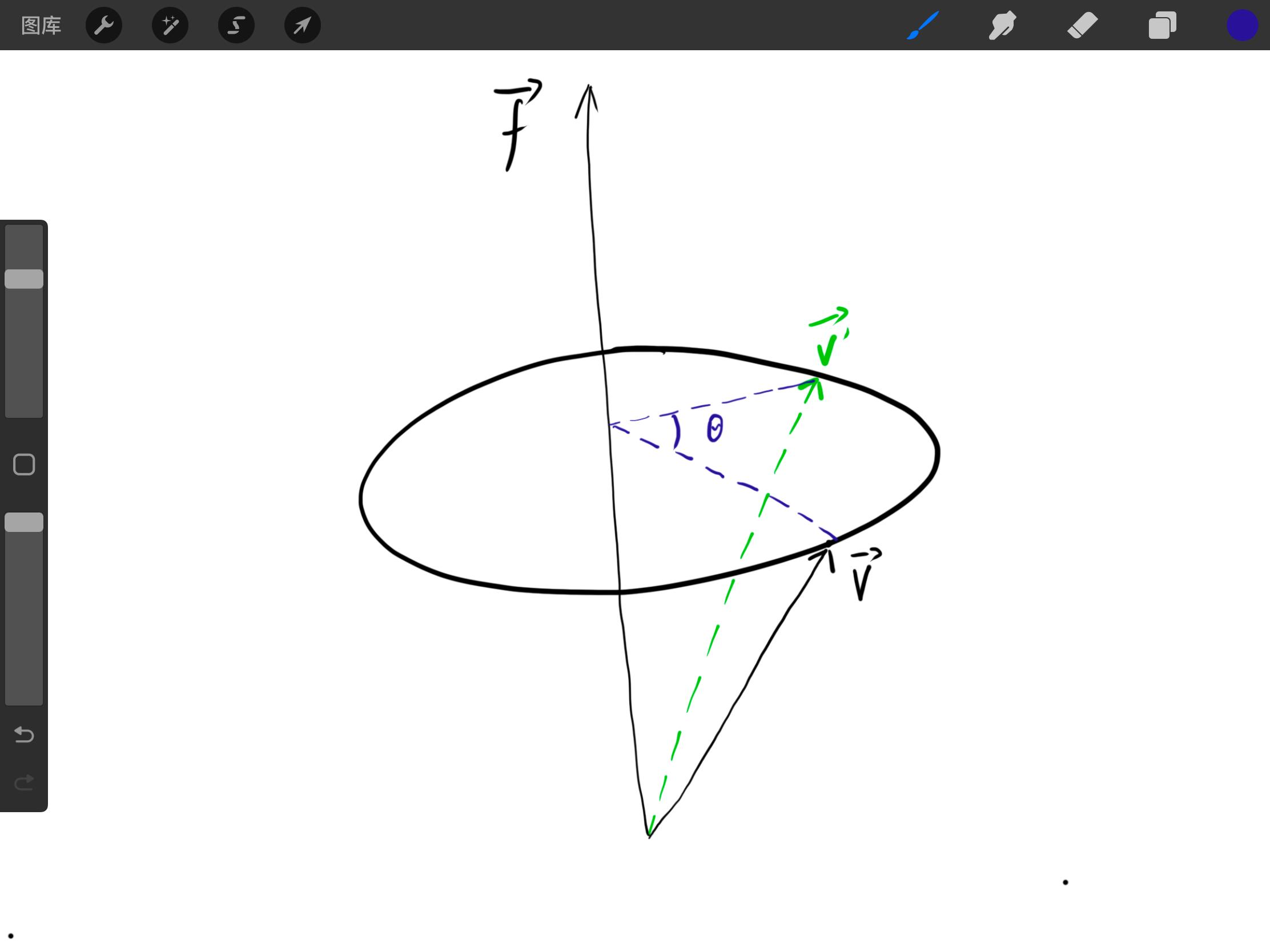
IMG_ECC68942A572-1

因為旋轉軸的長度並不影響旋轉，為了方便求解，定義 ∣∣f⃗∣∣=1||\vec {f}|| = 1。此時分解 v⃗\vec {v} 至平面（ v∥⃗\vec {v_\parallel} ）與旋轉軸（ v⊥⃗\vec {v_\perp} ）上。如下圖

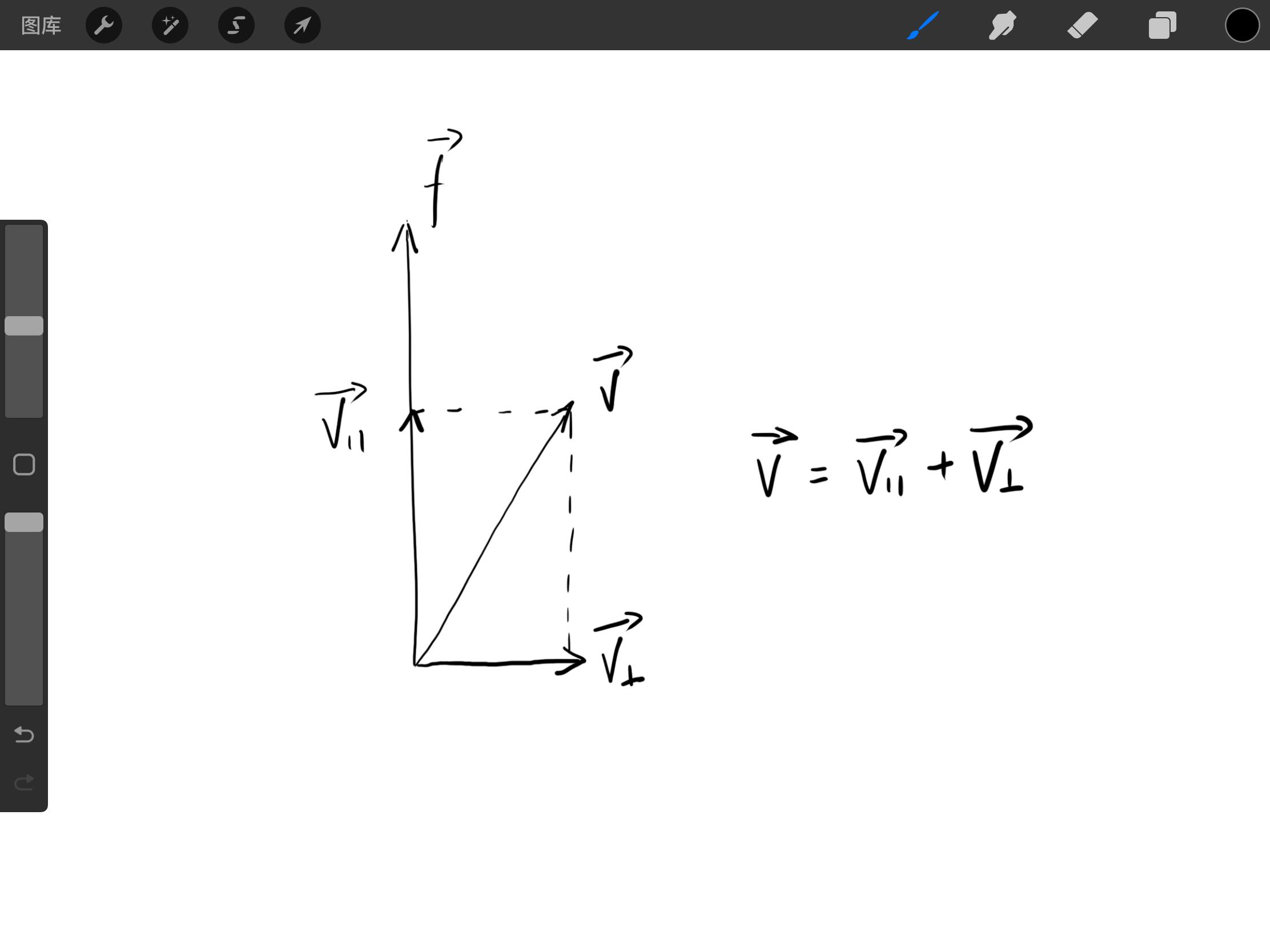
IMG_D190DB86E9D2-1

由於 v∥⃗\vec{v_\parallel} 可視為 v⃗\vec{v} 在 f⃗\vec{f} 上的投影，顯然可以使用點積來表示

即 v∥⃗=v⃗⋅f⃗∣∣f⃗∣∣f⃗∣∣f⃗∣∣\vec {v_\parallel} = \frac{\vec {v} \cdot \vec {f}}{||\vec {f}||} \frac {\vec {f}}{||\vec {f}||}

這裡解釋一下為什麼這麼寫，上面對於點積的介紹已經很明確了即點積的結果表示為向量 v 在 向量 f 上投影的模長乘以向量 f 的模長，也就是說我們如果需要單獨獲得 ∣∣v∥⃗∣∣|| \vec {v_\parallel} || 時需要將結果除以 ∣∣f⃗∣∣||\vec {f}|| ，而此時我們得到的是一個值而非向量，且 v∥⃗∥f⃗\vec {v_\parallel} \parallel \vec {f} 也就是兩者同向，於是我們可通過將值乘以 f⃗\vec {f} 的方向即可得到 v∥⃗\vec {v_\parallel}。而又因為 ∣∣f⃗∣∣||\vec {f}|| 為 1，則可化簡為

v∥⃗=(v⃗⋅f⃗)f⃗\vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f}

此時也可以得到 v⊥⃗\vec {v_\perp}

v⊥⃗=v⃗−v∥⃗=v⃗−(v⃗⋅f⃗)f⃗\vec {v_\perp} = \vec {v} - \vec {v_\parallel} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f}

目前已經得到的結果

{v∥⃗=(v⃗⋅f⃗)f⃗v⊥⃗=v⃗−(v⃗⋅f⃗)f⃗\begin{cases} \vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f} \\ \vec {v_\perp} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f} \end{cases}

現在我們對 v′⃗\vec {v^{\prime}} 進行分解，可發現 v∥⃗=v∥′⃗\vec {v_\parallel} = \vec {v^{\prime}_\parallel} ，唯一的不同在平面上的分解。

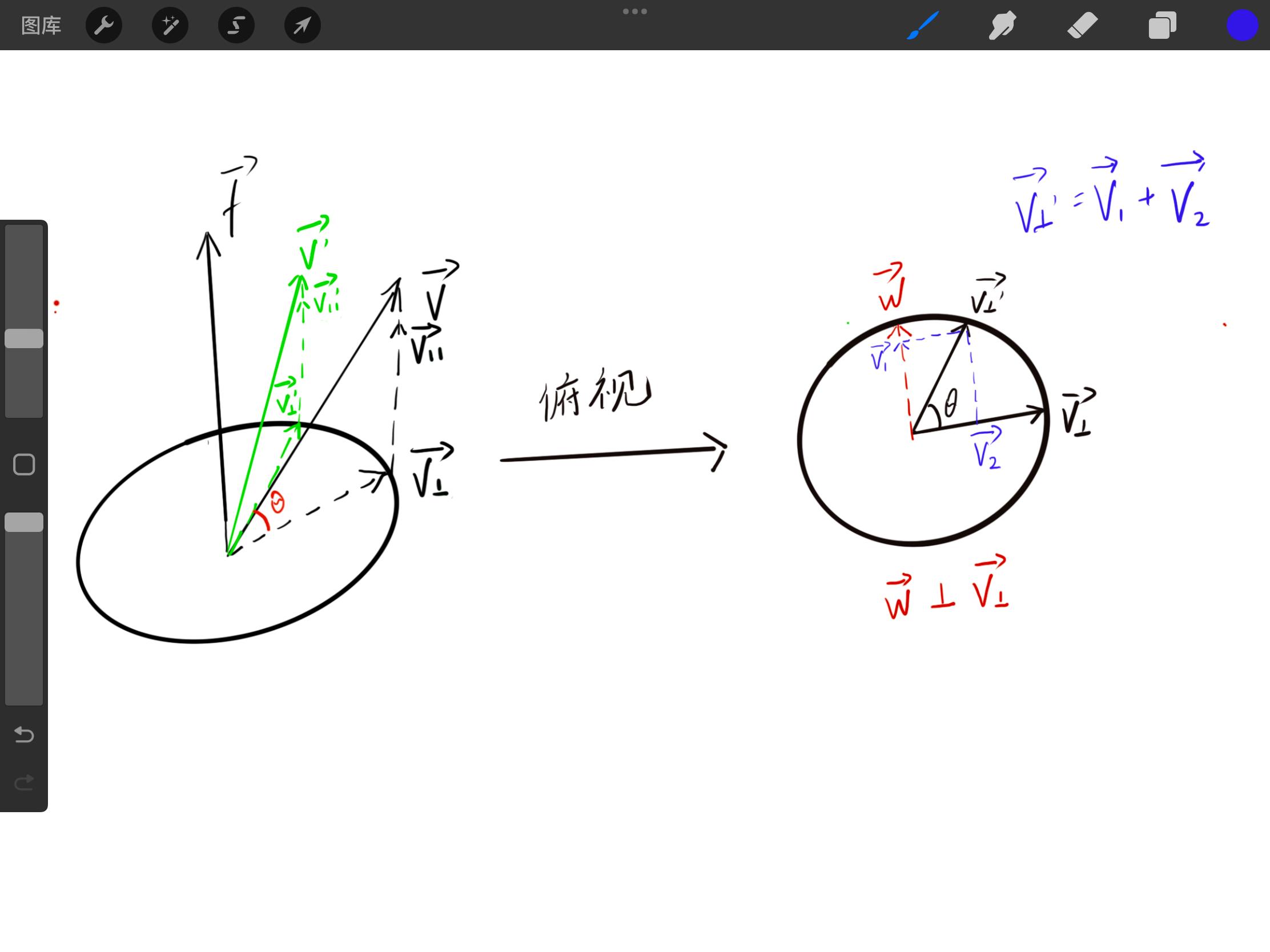
IMG_8ADF34270E8C-1

此時我們引入輔助向量 w⃗\vec {w} 該向量垂直於 v⊥⃗\vec {v_\perp}

∵{w⃗⊥f⃗w⃗⊥v⊥⃗∣∣f⃗∣∣=1∣∣w⃗∣∣=∣∣v⊥⃗∣∣\because \begin{cases} \vec {w} \perp \vec {f} \\ \vec {w} \perp \vec {v_\perp} \\ || \vec {f} || = 1 \\ || \vec {w} || = || \vec {v_\perp} || \\ \end{cases}
∴w⃗=f⃗×v⊥⃗\therefore \vec {w} = \vec {f} \times \vec {v_\perp}

因為我們最終的目標是通過 v⊥′⃗\vec {v^{\prime}_\perp} 求解 v′⃗\vec {v^{\prime}} ，那麼接下來需要分解 v⊥′⃗\vec {v^{\prime}_\perp} 為 v1⃗\vec {v_1} 與 v2⃗\vec {v_2} ，通過已知的 w⃗\vec {w} 與 v⊥⃗\vec {v_\perp} 來表達（求解思路和上面的 v 平行是相同的）

v1⃗=v⊥′⃗⋅w⃗∣∣w⃗∣∣w⃗∣∣w⃗∣∣=∣∣v⊥′⃗∣∣∣∣w⃗∣∣cos⁡(90°−θ)∣∣w⃗∣∣w⃗∣∣w⃗∣∣=w⃗sin⁡θ\vec {v_1} = \frac {\vec {v^{\prime}_\perp} \cdot \vec {w}}{||\vec {w}||} \frac {\vec {w}}{||\vec {w}||} = \frac {||\vec {v^{\prime}_\perp}|| || \vec {w} || \cos(90° - \theta)}{|| \vec {w} ||} \frac {\vec {w}}{||\vec {w}||} = \vec {w} \sin\theta

v2⃗=v⊥′⃗⋅v⊥⃗∣∣v⊥⃗∣∣v⊥⃗∣∣v⊥⃗∣∣=∣∣v⊥′⃗∣∣∣∣v⊥⃗∣∣cos⁡(θ)∣∣v⊥⃗∣∣v⊥⃗∣∣v⊥⃗∣∣=v⊥⃗cos⁡θ\vec {v_2} = \frac {\vec {v^{\prime}_\perp} \cdot \vec {v_\perp}}{||\vec {v_\perp}||} \frac {\vec {v_\perp}}{||\vec {v_\perp}||} = \frac {||\vec {v^{\prime}_\perp}|| || \vec {v_\perp} || \cos(\theta)}{|| \vec {v_\perp} ||} \frac {\vec {v_\perp}}{||\vec {v_\perp}||} = \vec {v_\perp} \cos\theta

v⊥′⃗=v1⃗+v2⃗=w⃗sin⁡θ+v⊥⃗cos⁡θ\vec {v^{\prime}_\perp} = \vec {v_1} + \vec {v_2} = \vec {w} \sin\theta + \vec {v_\perp} \cos\theta

∵w⃗=f⃗×v⊥⃗\because \vec {w} = \vec {f} \times \vec {v_\perp}

∴v⊥′⃗=v⊥⃗cos⁡θ+(f⃗×v⊥⃗)sin⁡θ\therefore \vec {v^{\prime}_\perp} = \vec {v_\perp} \cos\theta + (\vec {f} \times \vec {v_\perp}) \sin \theta

v′⃗=v⊥′⃗+v∥′⃗=v⊥⃗cos⁡θ+(f⃗×(v⃗−v∥⃗))sin⁡θ+v∥⃗\vec {v^{\prime}} = \vec {v^{\prime}_\perp} + \vec {v^{\prime}_\parallel} = \vec {v_\perp} \cos\theta + (\vec {f} \times (\vec {v} - \vec {v_\parallel})) \sin \theta + \vec {v_\parallel}

∵f⃗∥v∥⃗∴f⃗×v∥⃗=0\because \vec {f} \parallel \vec {v_\parallel} \therefore \vec {f} \times \vec {v_\parallel} = 0

v′⃗=v∥⃗+cos⁡θv⊥⃗+(f⃗×v⃗)sin⁡θ\vec {v^{\prime}} = \vec {v_\parallel} + \cos \theta \vec {v_\perp} + (\vec {f} \times \vec {v}) \sin \theta

∵{v∥⃗=(v⃗⋅f⃗)f⃗v⊥⃗=v⃗−(v⃗⋅f⃗)f⃗\because \begin{cases} \vec {v_\parallel} = (\vec {v} \cdot \vec {f})\vec {f} \\ \vec {v_\perp} = \vec {v} - (\vec {v} \cdot \vec {f})\vec {f} \end{cases}

∴v′⃗=(1−cos⁡θ)(f⃗⋅v⃗)f⃗+cos⁡θv⃗+sin⁡θ(f⃗×v⃗) \therefore \vec {v^{\prime}} = (1 - \cos \theta)(\vec {f} \cdot \vec {v}) \vec {f} + \cos \theta \vec {v} + \sin \theta (\vec {f} \times \vec {v})

求證結束，此時我們得到了軸角式的旋轉公式。

參考資料#

《動手學機器人學》（5）（一般形式旋轉矩陣公式）或（羅德里格旋轉公式）或（軸角法）證明 and 齊次坐標變換

載入中......
此文章數據所有權由區塊鏈加密技術和智能合約保障僅歸創作者所有。