同次座標と二次元図形の基本的な幾何変換の行列導出

同次座標#

“同次座標表示はコンピュータ・グラフィックスの重要な手段の一つであり、ベクトルと点を明確に区別することができ、またアフィン（線形）幾何変換を行うのにもより便利です。”—— F.S. Hill, JR。

引用の通り、同次座標の最大の特徴は、座標と ベクトル を区別できることです。

簡単に言えば、通常の直交座標系（またはデカルト座標系とも言えます）では、(x_A, y_A) は点 A を表すことも、ベクトル $\vec{oA}$ を表すこともできます。この曖昧な表現は、コンピュータに対して正確な抽象的な記述を行うのに適していません。

同次座標は、n 次元を n+1 次元に拡張することでこの問題を解決します。

2D デカルト座標の末尾に追加の変数 w を加えることで 2D 同次座標を形成できます。したがって、点 (X,Y) は同次座標では (x,y,w) となり、次のようになります。

X = x/w

Y = y/w

同次座標では、

点 A を表すには (x_A, y_A, 1)
ベクトル $\vec {oA}$ を表すには (x_A, y_A, 0)

w=1 と 0 を x/w に代入してみると、1 が点（位置）を、0 がベクトル（方向）を表す理由が理解できます。

さらに、ベクトル加法などの操作も容易になります。

もちろん、ベクトルと点を表すだけでなく、同次座標の導入は幾何変換（線形変換）を表現するのにも便利です。

例えば、同次座標を使用しない二次元平行移動は、下の図のようになります。

二次元図形の基本的な幾何変換#

二次元図形の変換は大きく分けて以下の五つのカテゴリーに分類されます —— 平行移動（Translate）、スケーリング（Scale）、回転（Rotate）、反射（Reflect）、およびせん断（shear）

1. 平行移動#

点 (x, y) から (x + dx, y + dy) への移動を表します。

同次座標を導入すると、(x, y, 1) が変形して (x + dx, y + dy, 1) になります。

この時、線形変換をツールとして変換過程を記述でき、変換行列を導入すると、この問題は変換行列を求めることに変わります。

既知のこと:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x + dx \\ y + dy \\ 1 \end{pmatrix}

得られる式は次の通りです。

\begin{cases} ax + by + c = x + dx \\ dx + ey + f = y + dy \\ gx + hy + i = 1 \end{cases}

解得られる変換行列は次の通りです。

\begin{pmatrix} 1 & 0 & dx \\ 0 & 1 & dy \\ 0 & 0 & 1 \end{pmatrix}

したがって、数学的な観点からこの変換行列を使用して平行移動の過程を記述できます。

2. スケーリング#

点 (x, y) から (sx*x, sy*y) への変換を表します。sx と sy は定数です。

同次座標を導入すると、(x, y, 1) が変形して (sx*x, sy*y, 1) になります。

変換行列を導入します。

既知のこと:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} sx * x \\ sy * y \\ 1 \end{pmatrix}

得られる式は次の通りです。

\begin{cases} ax + by + c = sx * x \\ dx + ey + f = sy * y \\ gx + hy + i = 1 \end{cases}

解得られる変換行列は次の通りです。

\begin{pmatrix} sx & 0 & 0 \\ 0 & sy & 0 \\ 0 & 0 & 1 \end{pmatrix}

3. 回転#

回転を説明するには単位円を導入する必要があります。

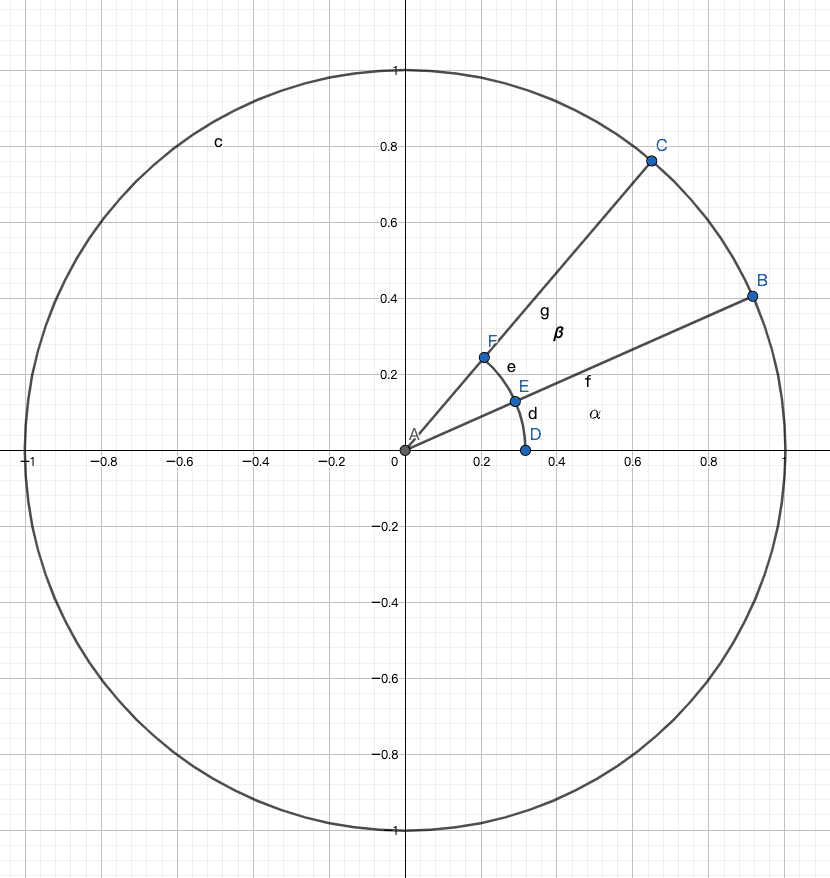
図のように、点 B が点 C に回転し、AB と X 軸の間の角度を α、AC と AB の間の角度を β とします。

B 点の座標は (cosα, sinα) で、C 点の座標は (cos (α + β), sin (α + β)) です。

C 点の座標を展開すると、C 点は (cosα cosβ - sinα sinβ, sinα cosβ + cosα sinβ) となります。

B 点の座標を (x, y) とし、C 点の座標は (x cosβ - y sinβ, y cosβ + x sinβ) となります。

同次座標を導入すると、(x, y, 1) が変形して (x cosβ - y sinβ, y cosβ + x sinβ, 1) になります。

変換行列を導入します。

既知のこと:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} xcosβ - ysinβ \\ ycosβ + xsinβ \\ 1 \end{pmatrix}

得られる式は次の通りです。

\begin{cases} ax + by + c = xcosβ - ysinβ \\ dx + ey + f = ycosβ + xsinβ \\ gx + hy + i = 1 \end{cases}

解得られる変換行列は次の通りです。

\begin{pmatrix} cosβ & -sinβ & 0 \\ sinβ & cosβ & 0 \\ 0 & 0 & 1 \end{pmatrix}

4. 反射#

数学において、反射は物体をその鏡像に変換する写像です。平面図形を反射するには、「鏡」として直線（反射軸）が必要であり、三次元空間での反射には平面を鏡として使用します。

引用に基づくと、反射は X 軸に対する反射と Y 軸に対する反射に分けられますが、実際には中心反射（点反射）という概念も存在します。

X 軸に対する反射#

点 (x, y) から点 (x, -y) への変換を表します。

既知のこと:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ -y \\ 1 \end{pmatrix}

得られる式は次の通りです。

\begin{cases} ax + by + c = x \\ dx + ey + f = -y \\ gx + hy + i = 1 \end{cases}

解得られる変換行列は次の通りです。

\begin{pmatrix} 1 & 0 & 0 \\ 0 & -1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

Y 軸に対する反射#

点 (x, y) から点 (-x, y) への変換を表します。

既知のこと:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} -x \\ y \\ 1 \end{pmatrix}

得られる式は次の通りです。

\begin{cases} ax + by + c = -x \\ dx + ey + f = y \\ gx + hy + i = 1 \end{cases}

解得られる変換行列は次の通りです。

\begin{pmatrix} -1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

点 (p, q) に対する反射#

点 (x, y) から点 (2p-x, 2q-y) への変換を表します。

既知のこと:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} 2p-x \\ 2q-y \\ 1 \end{pmatrix}

得られる式は次の通りです。

\begin{cases} ax + by + c = 2p-x \\ dx + ey + f = 2q-y \\ gx + hy + i = 1 \end{cases}

解得られる変換行列は次の通りです。

\begin{pmatrix} -1 & 0 & 2p \\ 0 & -1 & 2q \\ 0 & 0 & 1 \end{pmatrix}

5. せん断#

定義は図に見られる通りで、実際には図形がある方向に歪むようなものです。以下に推導過程を示します。注意すべきは α と β の範囲が [0, 90°) であることです。

Y 軸を依存軸としたせん断変換#

点 (x, y) から点 (x + y.tanα, y) への変換を表します。

既知のこと:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x+y.tanα \\ y \\ 1 \end{pmatrix}

得られる式は次の通りです。

\begin{cases} ax + by + c = x+y.tanα \\ dx + ey + f = y \\ gx + hy + i = 1 \end{cases}

解得られる変換行列は次の通りです。

\begin{pmatrix} 1 & tanα & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}

X 軸を依存軸としたせん断変換#

点 (x, y) から点 (x, y + x.tanβ) への変換を表します。

既知のこと:

\begin{pmatrix} a & b & c \\ d & e & f \\ g & h & i \end{pmatrix} \begin{pmatrix} x \\ y \\ 1 \end{pmatrix} = \begin{pmatrix} x \\ y + x.tanβ \\ 1 \end{pmatrix}

得られる式は次の通りです。

\begin{cases} ax + by + c = x \\ dx + ey + f = y + x.tanβ \\ gx + hy + i = 1 \end{cases}

解得られる変換行列は次の通りです。

\begin{pmatrix} 1 & 0 & 0 \\ tanβ & 1 & 0 \\ 0 & 0 & 1 \end{pmatrix}