图形学
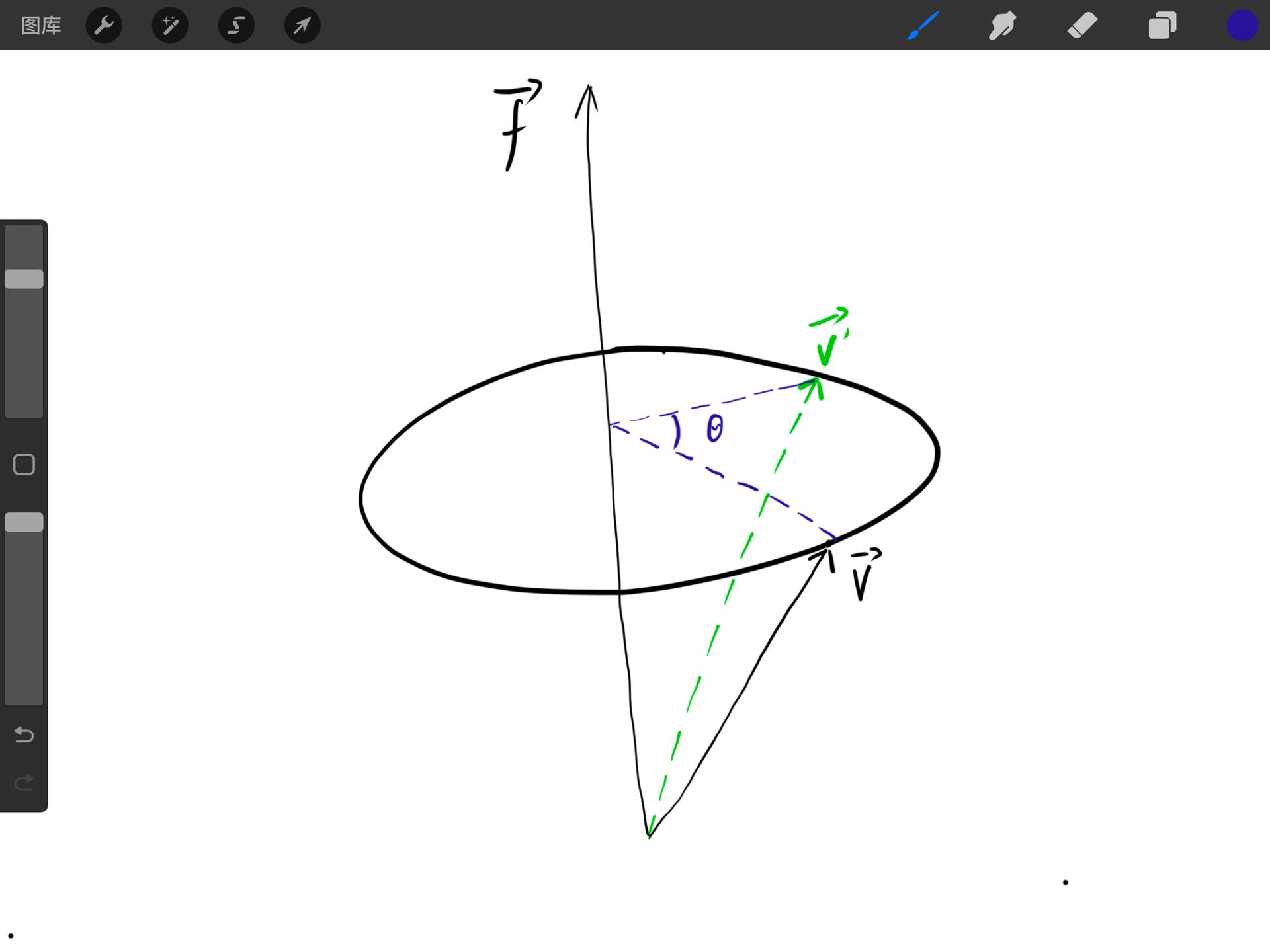
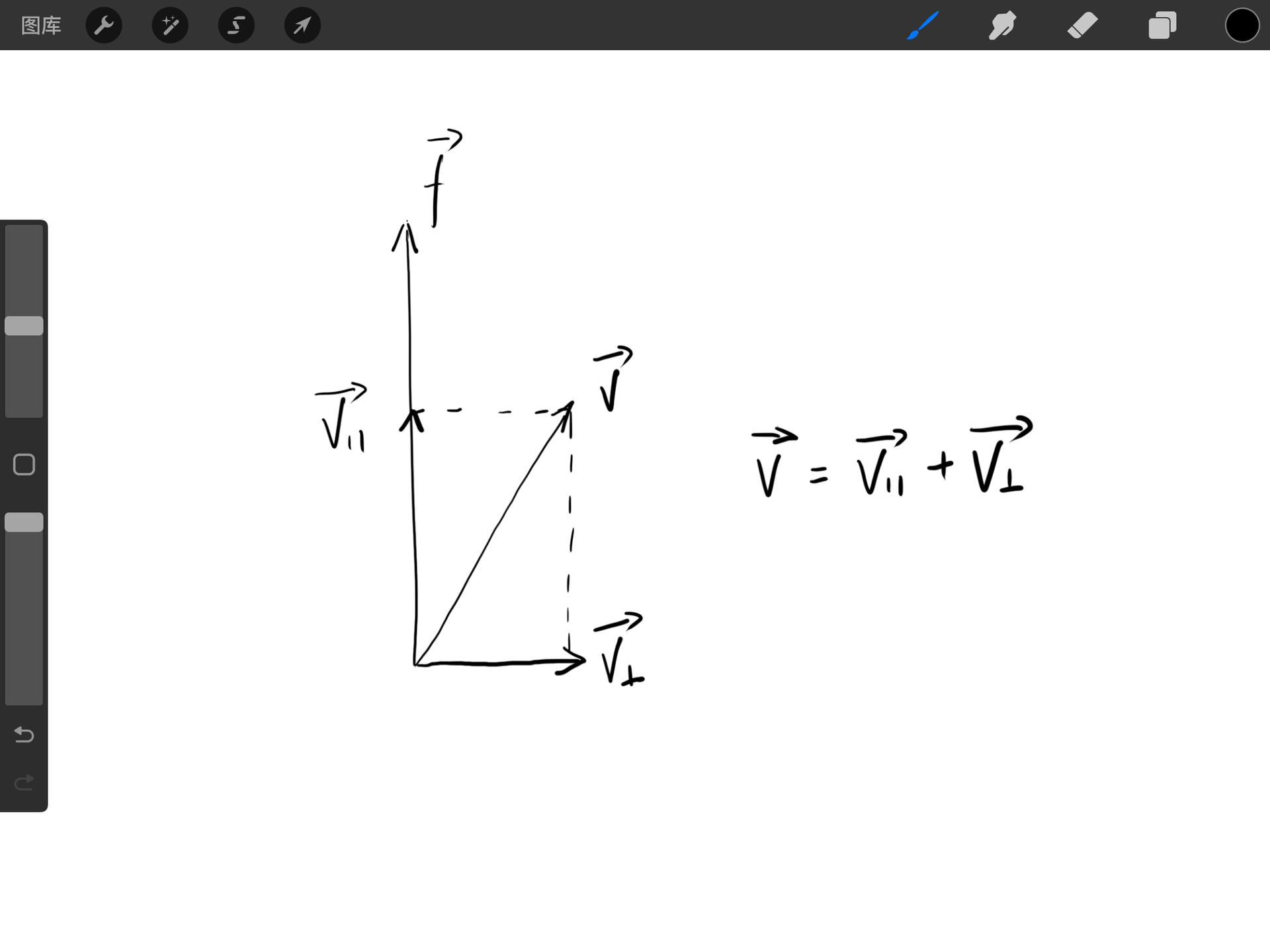
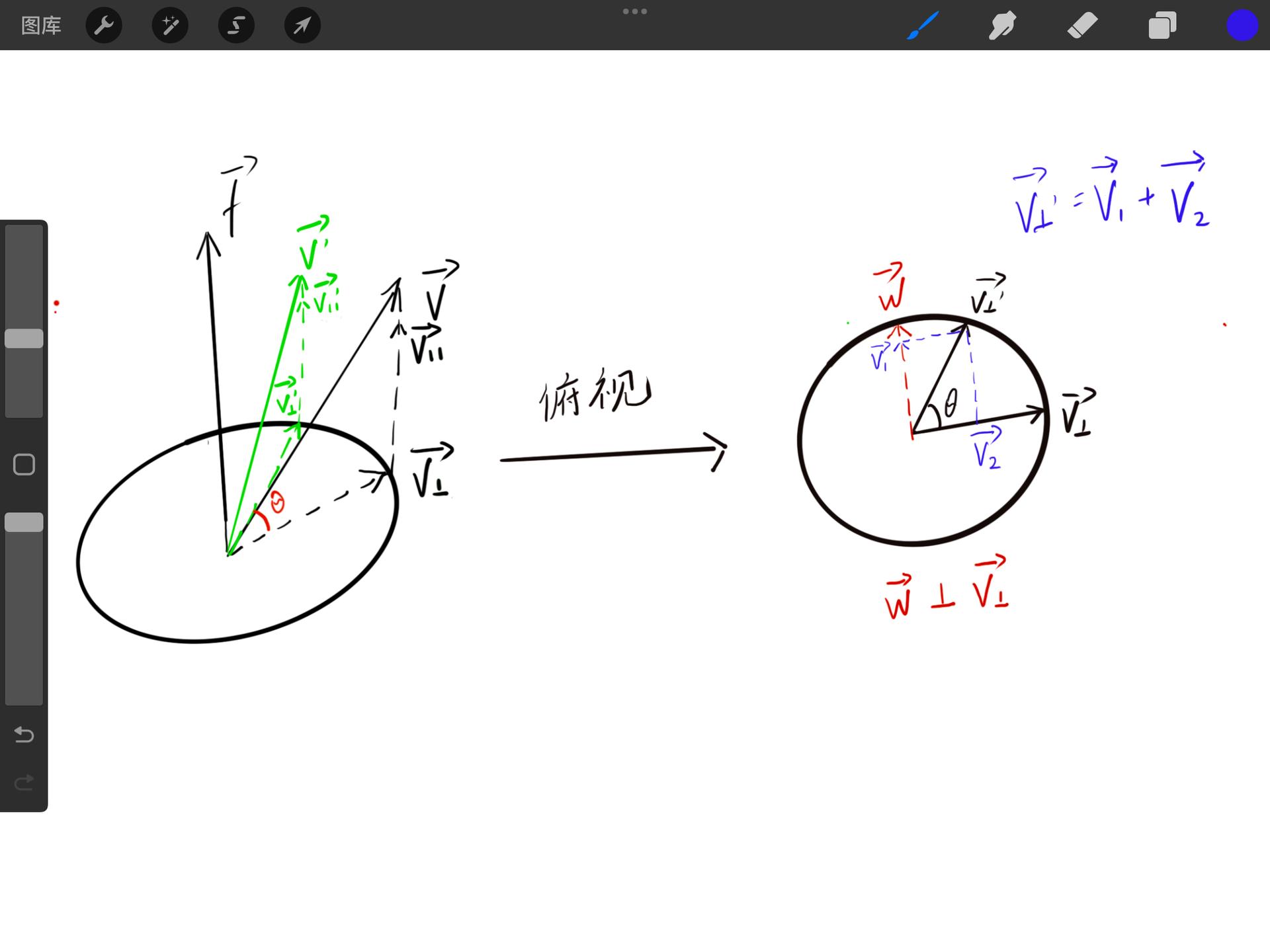
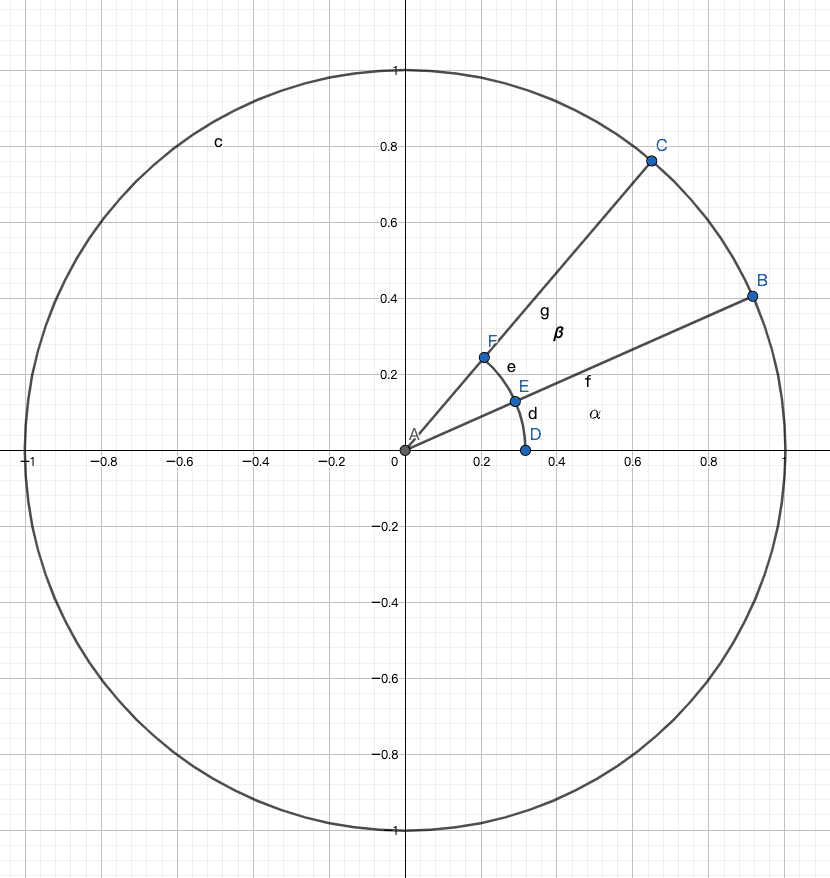
罗德里格旋转公式(轴角法)
前言 阅读本文需要一些前置知识,需理解向量点积与叉积的基本知识。以下给出大致定义(因为矩阵在这里用不到,就不写矩阵形式了)以帮助理解
向量点积
\vec {v} \cdot \vec {j} = ||\vec {v}|| ||\vec {j}|| \cos \theta 几何…
三维图形基本几何变换的矩阵推导
前言 此文是 齐次坐标与二维图形基本几何变换的矩阵推导 的衍生。理解二维的变换就能轻松推导三维的。
三维图形基本几何变换
平移
描述从点 (x, y, z) 到 (x + dx, y+ dy, z + dz)
引入齐次坐标,可表述为 (x, y, z, 1) 变形推导为 (x +…
齐次坐标与二维图形基本几何变换的矩阵推导
齐次坐标 “齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”—— F.S. Hill, JR。
正如引用中所说,齐次坐标最大的特点在于它的存在可以区分描述 坐标 与 向量
简单的来说,在普通的直角坐标系…
欧拉角与万向锁
说明 前置阅读:三维图形基本几何变换的矩阵推导
对于在三维空间里的一个参考系,任何坐标系的取向,都可以用三个欧拉角来表现。(三个欧拉角变换可以描述当前物体的姿态)
俯仰(绕 z 轴旋转)、偏航(绕 y 轴旋转)、滚动(绕 x 轴旋转)了解下就行
由于线性变换不符合交换律…