数学
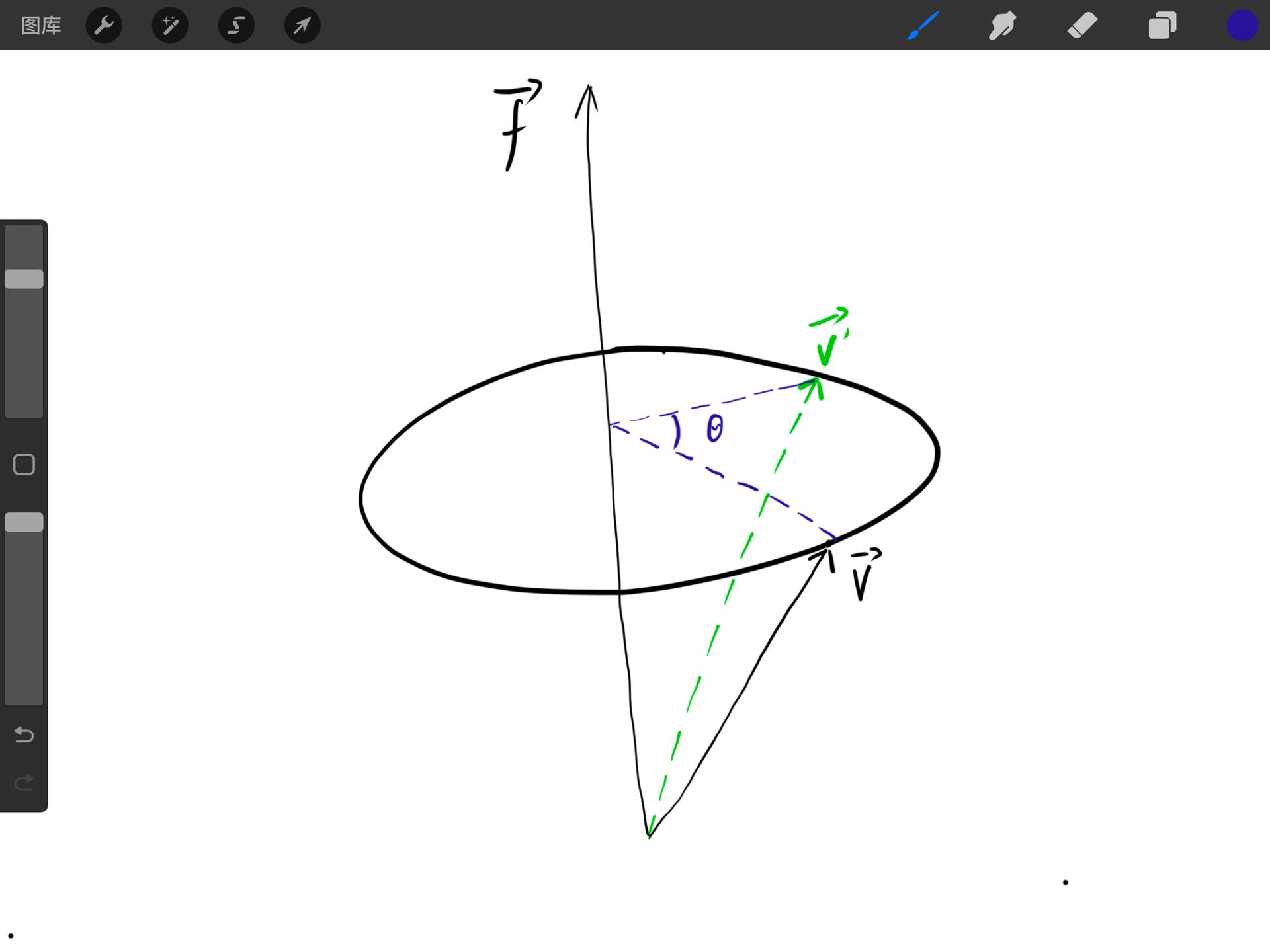
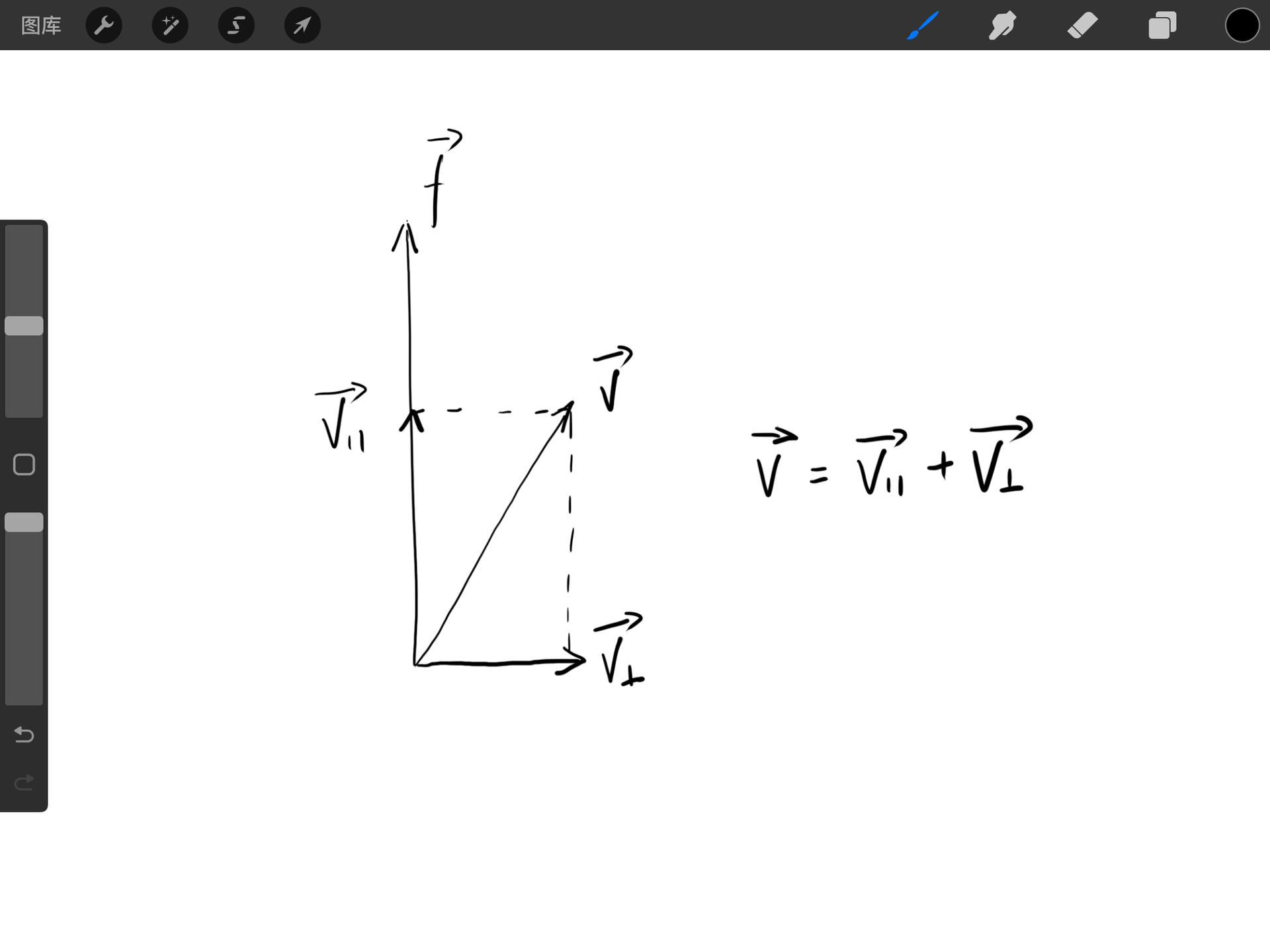
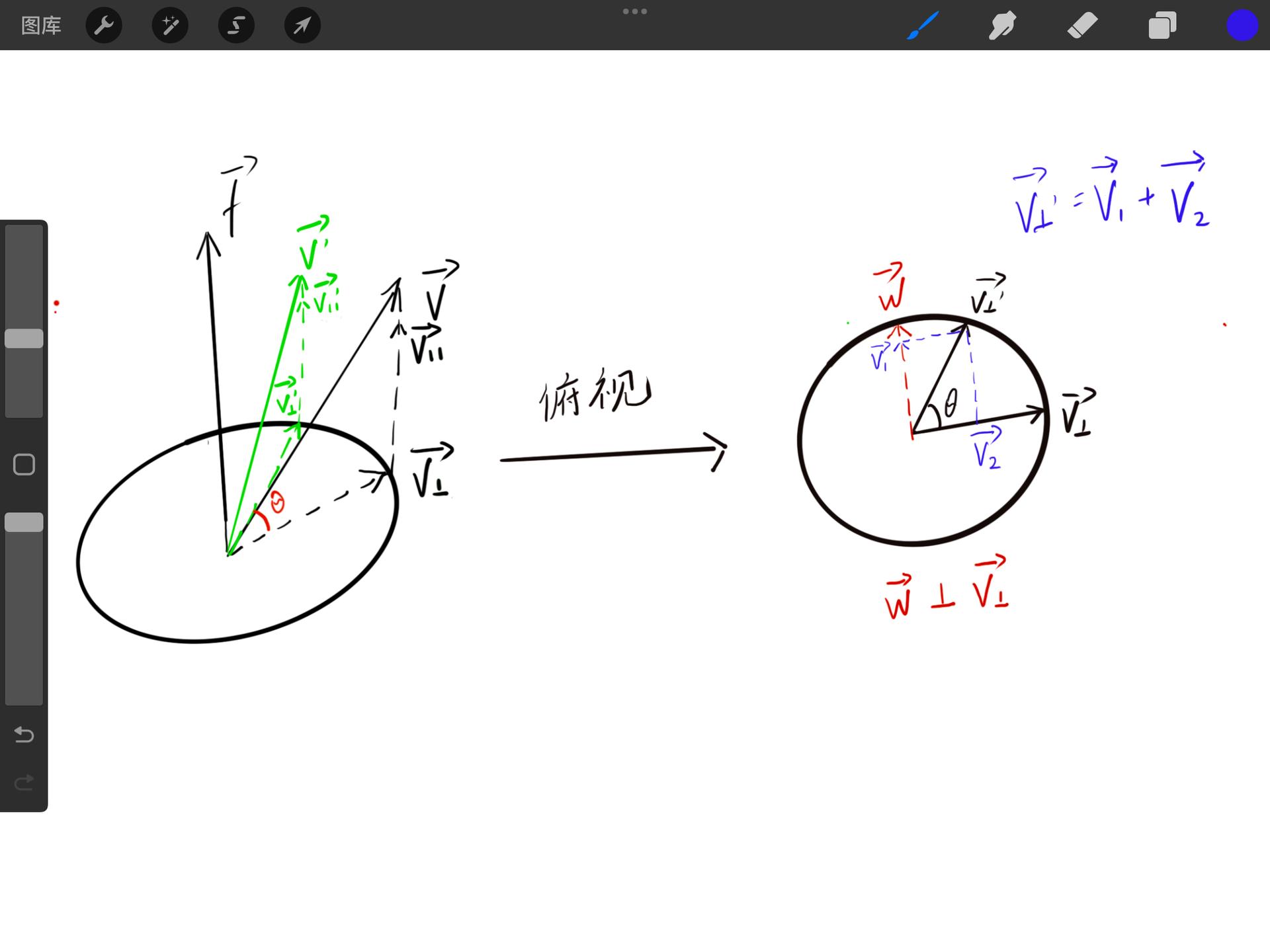
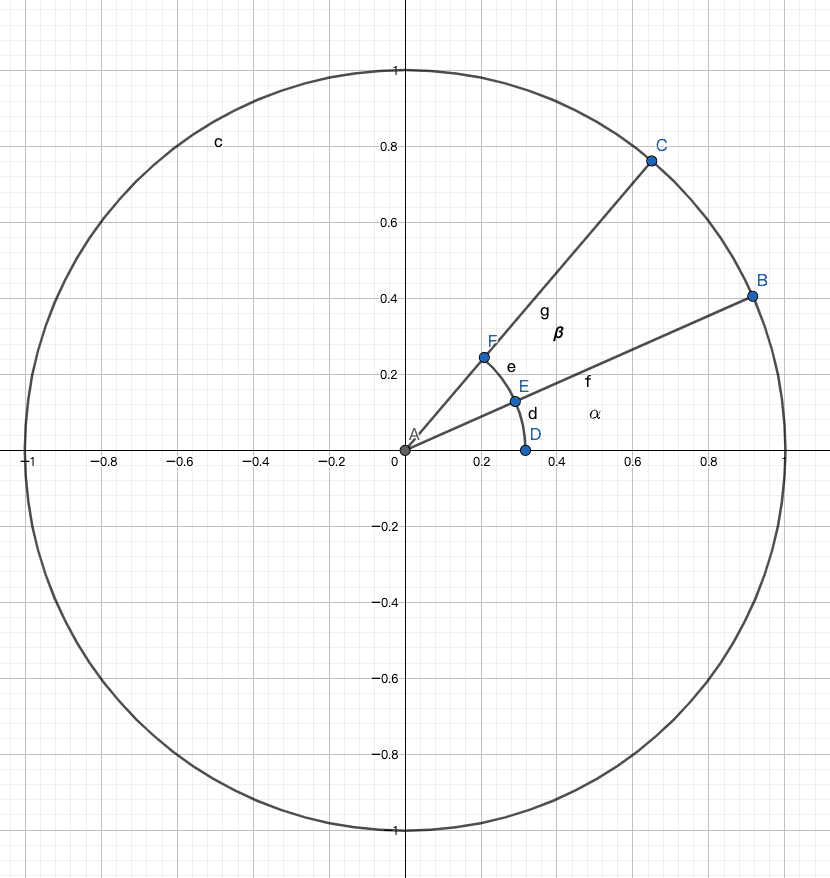
罗德里格旋转公式(轴角法)
前言 阅读本文需要一些前置知识,需理解向量点积与叉积的基本知识。以下给出大致定义(因为矩阵在这里用不到,就不写矩阵形式了)以帮助理解
向量点积
\vec {v} \cdot \vec {j} = ||\vec {v}|| ||\vec {j}|| \cos \theta 几何…
三维图形基本几何变换的矩阵推导
前言 此文是 齐次坐标与二维图形基本几何变换的矩阵推导 的衍生。理解二维的变换就能轻松推导三维的。
三维图形基本几何变换
平移
描述从点 (x, y, z) 到 (x + dx, y+ dy, z + dz)
引入齐次坐标,可表述为 (x, y, z, 1) 变形推导为 (x +…
齐次坐标与二维图形基本几何变换的矩阵推导
齐次坐标 “齐次坐标表示是计算机图形学的重要手段之一,它既能够用来明确区分向量和点,同时也更易用于进行仿射(线性)几何变换。”—— F.S. Hill, JR。
正如引用中所说,齐次坐标最大的特点在于它的存在可以区分描述 坐标 与 向量
简单的来说,在普通的直角坐标系…
从傅立叶级数到傅立叶变换
Games101 的第 6 讲内有涉及到傅立叶变换的内容,课后花了点功夫才搞明白这东西(虽然大学学过但也忘得差不多了),于是写下这篇文章用以记录学习心得。 参考资料中我强烈推荐 DR_CAN 老师的《纯干货数学推导》系列!本文大多都是他课程内的笔记。
本文将从以下几个方面…
泰勒展开式(待补全)
泰勒级数是在数学中极其强大的函数近似工具 —— 3Blue1Brown 这两天重新学习了关于泰勒展开式的内容,决定趁热打铁水一篇文章出来作为学习记录。
泰勒定理的大致思想为如果一个函数足够光滑,在已知函数某一点各阶导数的前提下…